数字输入优化与外推方法解析

#NLP

元数据

数字输入优化的核心方法

在机器学习中，如何设计数字输入的表示方式对模型性能和扩展能力至关重要。本文探讨了几种优化方法，包括进制表示、直接外推、线性内插，以及进制转换，并分析了它们的优缺点。

✅ 数字输入的进制表示与直接外推

  1. 进制表示：

    • 将一个整数拆分为多维向量。例如，1000以内的整数可以用三维向量 [a, b, c] 表示，其中 a 是百位数，b 是十位数，c 是个位数。
    • 若需要进一步缩小跨度，可以采用更小的基数（如8进制或2进制），但会增加输入维度。

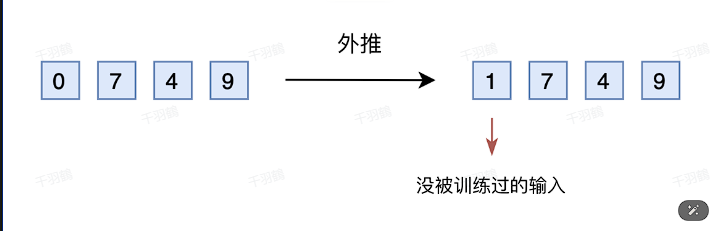
  2. 直接外推：

    • 当需要扩展范围（如从1000扩展到2000），可以增加维度，如将原三维向量扩展为四维。
    • ⚠ 警告：直接外推可能导致模型性能下降，因为新增维度未经过训练，模型难以适应。 Pasted image 20250407171715.png

⚠ 线性内插与进制转换的优化策略

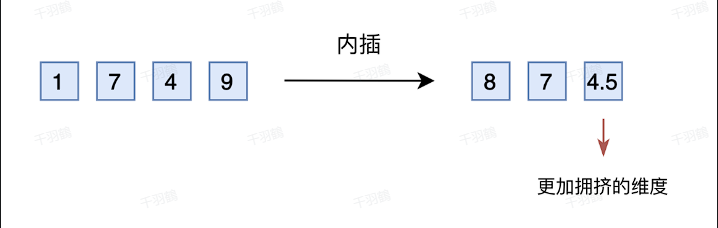
  1. 线性内插：
    • 将扩展范围压缩到原范围，例如将2000以内的数除以2，压缩到1000以内。
    • 示例：1749变为874.5，输入为 [8, 7, 4.5]。
    • 优点：避免新增维度。
    • 缺点：映射关系拥挤，不同维度的分布不均衡，需微调模型以适应新的映射。
      Pasted image 20250407171727.png
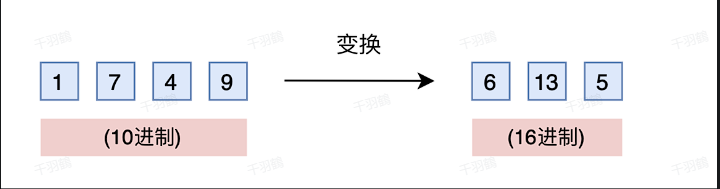
  2. 进制转换：
    • 使用更高的进制以保持输入维度不变。例如，16进制编码可以用三维向量表示0~4095的范围。
    • 优点：无需新增维度，且比较规则一致（如875 > 874在10进制和16进制下均成立）。
    • 💡 启发点：通过进制转换提高模型扩展性，同时减少训练复杂度。
      Pasted image 20250407171735.png

常见错误提醒

直接外推的风险：

表格数据整理

方法 优点 缺点
进制表示 简单易懂，适合小范围数字 增加基数会导致维度增加
直接外推 扩展范围灵活 模型性能下降风险高
线性内插 避免新增维度 映射拥挤，不同维度分布不均
进制转换 保持输入维度不变，扩展性强 数字跨度变大，可能需调整模型参数

📈 趋势预测

随着数据范围进一步扩大，进制转换可能成为主流解决方案，因为它能有效平衡输入维度与模型性能。未来研究可能集中在如何自动选择最优进制或动态调整基数，以适应不同任务需求。

[思考]板块

  1. 如何设计一种动态进制转换机制，使得模型可以根据输入范围自动调整编码方式？
  2. 在处理超大范围数字时，是否可以结合分块处理（如分段映射）与进制转换来优化模型性能？
  3. 能否开发一种预训练模型，使其对未训练范围的数据具有更强的泛化能力？

行动清单

原文出处：《长度外推优化》