Transformer绝对位置编码详解与改进分析

元数据

分类：深度学习 / NLP
标签：Transformer、位置编码、深度学习、自然语言处理
日期：2025年3月2日

核心内容总结

Transformer模型中的绝对位置编码是通过正弦和余弦函数构造的一种固定编码方式，主要用于为输入序列的每个位置注入位置信息。这种编码方式具有生成规律性和一定的外推能力，但在实际使用中也存在一些局限性，比如方向性信息的丢失和相对位置表达能力的破坏。

重点内容解析

1. 位置编码的定义与公式

Transformer位置编码是通过正弦函数和余弦函数交替生成的，具体公式如下：

P E_{t} = [\sin (w_{0} t), \cos (w_{0} t), \sin (w_{1} t), \cos (w_{1} t), \dots, \sin (w_{2 d_{m o d e l} - 1} t), \cos (w_{2 d_{m o d e l} - 1} t)]

其中， $t$ 表示序列中的具体位置， $w_{k}$ 是频率参数， $d_{m o d e l}$ 表示模型的维度。
这种编码方式确保每个位置的编码值都位于 $[- 1, 1]$ 范围内。

💡 启发点：正弦和余弦函数具有周期性和规律性，因此这种编码方式能够在一定程度上支持模型的外推能力。

2. 编码可视化特点

通过对长度为100、维度为512的序列进行可视化，可以观察到以下现象：

每个位置编码值在 $[- 1, 1]$ 范围内。
随着频率的降低（即波长变长），图像右半部分颜色变化趋于平稳。
左半部分由于高频率的影响，颜色交替更为频繁。

📈 趋势预测：频率越高的位置编码对结果影响越大，而低频部分主要用于捕捉全局信息。

3. 缺点与局限性

尽管正弦位置编码具有生成规律，但其在以下方面存在不足：

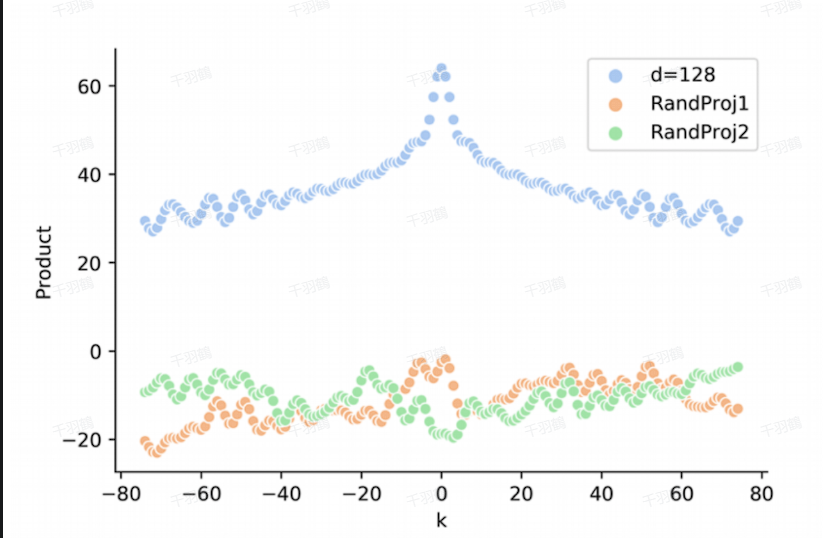
无方向性：由于位置编码的点积无向性，无法区分前后关系。例如：
$P E_{t}^{T} \cdot P E_{t + Δ t} = P E_{t}^{T} \cdot P E_{t - Δ t}$
即，两个位置编码之间的点积仅取决于距离 $Δ t$ ，而不包含方向信息。
相对位置信息的破坏：当位置编码与输入嵌入（Input Embedding）一起被投影到注意力机制中时，正弦位置编码的相对位置表达能力可能被投影矩阵破坏。

⚠ 常见错误：直接假设正弦位置编码能完全表达相对位置信息，而忽略其方向性不足的问题。

4. 改进方向

为了克服上述缺点，一些后续模型（如BERT）引入了可学习的位置编码，通过训练获得更灵活的位置信息表示，从而提升模型性能。

示例代码

以下是一个生成正弦位置编码的Python代码示例：

import numpy as np

def get_positional_encoding(seq_len, d_model):
    position = np.arange(seq_len)[:, np.newaxis]
    div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model))
    pos_encoding = np.zeros((seq_len, d_model))
    pos_encoding[:, 0::2] = np.sin(position * div_term)
    pos_encoding[:, 1::2] = np.cos(position * div_term)
    return pos_encoding

# 示例：生成长度为100、维度为512的位置编码
pos_encoding = get_positional_encoding(100, 512)
print(pos_encoding)

[思考] 延伸问题

如何设计一种新的位置编码方式，使其既能保留绝对位置信息，又能增强相对位置信息的表达？
可学习的位置编码是否会引入额外的过拟合风险？如何平衡灵活性与泛化能力？
在低资源语言或小规模数据集上，固定位置编码与可学习位置编码哪种更具优势？

原始出处：本文内容参考于Transformer模型中关于绝对位置编码的技术文档与相关研究分析。