SARSA-λ与Q-learning对比

分类

自动推断

标签

• 强化学习
• SARSA-λ
• Q-learning

日期

2025年4月11日

内容概述

SARSA-λ和Q-learning是两种常见的强化学习算法。本文将对这两种算法进行深入分析，探讨它们的优缺点及应用场景。

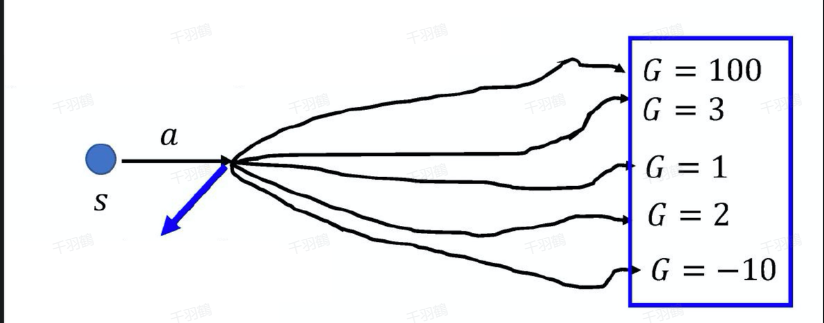
SARSA-λ算法

SARSA-λ结合了蒙特卡洛方法和时序差分算法的优点。蒙特卡洛方法无偏但方差较大，因为每一步状态转移的奖励不确定性较高。而时序差分算法关注单步状态转移，方差小但有偏，因为使用下一个状态的估计值而非真实值。

SARSA-λ通过考虑多步时序差分来折中这两者，更新公式为：

Q-learning算法

Q-learning基于最优贝尔曼方程估计最优动作价值。其更新公式为：

Q-learning每次选择下一个状态动作价值最高的值和即时奖励来作为当前状态最优动作价值的估计。

算法流程

Q-learning算法流程：

✅ 初始化 $Q(s,a)$

⚠ for 序列 $e=1\to E$

❗ 得到初始状态 $s$

⚠ for 时间步 $t=1\to T$

❗ 用 $ϵ$-贪婪策略选择当前状态 $s$ 下的动作 $a$

❗ 更新 $Q(s,a)$

❗ 状态更新 $s\leftarrow s^{\prime }$

⚠ end for

⚠ end for

常见错误

在实现Q-learning时，需谨慎处理状态转移和动作选择，避免因选择策略不当导致价值估计偏差。

代码示例

class QLearning:
    """ Q-learning算法 """
    def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):
        self.Q_table = np.zeros([nrow * ncol, n_action])
        self.n_action = n_action
        self.alpha = alpha
        self.gamma = gamma
        self.epsilon = epsilon
    
    def take_action(self, state):
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.n_action)
        else:
            action = np.argmax(self.Q_table[state])
        return action
    
    def best_action(self, state):
        Q_max = np.max(self.Q_table[state])
        a = [0 for _ in range(self.n_action)]
        for i in range(self.n_action):
            if self.Q_table[state, i] == Q_max:
                a[i] = 1
        return a

💡 启发点：Q-learning通过选择价值最高的动作来优化策略，是一种有效的探索和利用平衡方法。

思考

• 在复杂环境中，如何有效地选择合适的折扣因子($\gamma$)？
• SARSA-λ在实际应用中有哪些具体场景？
• 是否有可能结合其他算法进一步提高学习效率？

原始出处：[SARSA-λ与Q-learning算法分析]

行动清单

• 探索不同环境下两种算法的性能表现。
• 调整参数，观察其对学习效果的影响。
• 研究其他强化学习算法与其结合的可能性。

📈 趋势预测：随着机器学习的发展，强化学习算法将越来越多地应用于自动驾驶、机器人控制等领域，其优化效率将不断提升。

后续追踪

• 进一步研究SARSA-λ与Q-learning在连续状态空间中的应用。
• 探讨两种算法在多智能体系统中的协同学习效果。